القوة والحركات المنحنية. الاجابة عن أهم الأسئلة

القوة والحركات المنحنية، هو موضوع في الفيزياء، يركز على دراسة تأثير القوة على الأجسام، التي تتحرك على مسارات منحنية. يتضمن هذا الدرس: دراسة السرعة والقوة في وضعيات مختلفة، دراسة حركة دائرية منتظمة، دراسة حركة القذائف.

ملاحظة: توجد وثيقة التلميذ بصيغة الـ PDF في نهاية المقال.

I ـ نشاطات أولية:

نقذف كرة حديدية، بحيث تسقط قريبا من كرية صغيرة موضوعة على الأرض (الشكل).

ـ حسب رأيك ما هو شكل التصوير المتعاقب لحركة مركز الكرة ؟ مثله بعناية.

الاجابة:

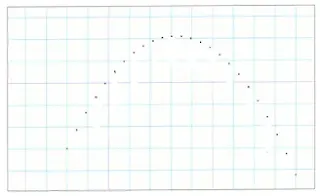
ـ حسب رأيك، وبأخذ بعين الاعتبار ما تعلمته، كيف يجب التأثير على الجسم للحصول على هذه الحركة ؟ مثل بأسهم على التصوير المتعاقب هذا التأثير، وارفق انشائك بشرح مختصر.

الاجابة:

     يكون مسار حركة مركز القذيفة (S) منحنيا (على شكل قطع مكافئ)، تتناقص قيمة السرعة أثناء الصعود، وتتزايد أثناء النزول.

    ان الفعل المتسبب في حركة القذيفة هو جذب الأرض للجسم. يمثل هذا الفعل بقوة تدعى" الثقل "، ويرمز لها بالرمز \(\vec{F}_{T/S}\)

نريد الان أن تبقى سرعة مركز جسم ثابتة، ولكن على مسار دائري.
أ ـ حسب رأيك، ما هو الشكل الجديد للتصوير المتعاقب لمركز الجسم ؟ أرسم بعناية على كراسك هذا الشكل.
ب ـ حسب رأيك، كيف يمكن التأثير على الجسم للحصول على هذه الحركة ؟ مثل بسهم على الرسم السابق، هذا التأثير، وأرفق رسمك بشرح مختصر.

الاجابة:

للحصول على حركة دائرية منتظمة، يجب التأثير على الجسم بقوة ثابتة الشدة تبقى عمودية على المسار الدائري لمركز الجسم، ومتجهة نحو مركز المسار.

إذا كان المسار دائري، وسرعة المتحرك ثابتة القيمة، ومتغيرة المنحى والجهة خلال الحركة، نقول عن حركة جسم أنها دائرية منتظمة، حيث أن شعاع السرعة في الحركة الدائرية المنتظمة يحافظ على قيمته، ويتغير منحاه وجهته في كل لحظة، كما يوضحه الشكل التالي:

     كما أن شعاع القوة يكون في كل لحظة عموديا على شعاع السرعة، وموجها نحو التقعر الداخلي للمسار. أي أن شعاع القوة يكون عموديا على المماس للمسار في كل نقطة وفي كل لحظة، أي أنه منطبق في كل لحظة على نصف قطر الدائرة، ومتجها نحو مركزها، (لأن نصف قطر دائرة عمودي على المماس).

II ـ دراسة حركة مقذوف أفقيا:

نشاط

ندفع كرة صغيرة على طاولة أفقية ملساء نحو حافتها لنتطلق في الهواء، ثم تسقط على الأرض وفق مسار منحني، يمثل الشكل تسجيلا متعاقبا لحركة الكرة بفارق زمني بين كل تسجيلين متتاليين قدره 0,2 ثانية

1 ـ ماهي طبيعة مسار النقطة M ؟

2 ـ أكمل الجدول التالي؟

M10	M9	M8	M7	M6	M5	M4	M3	M2	M1	M0	المواضع
									0,2	0	t(s)
											x(m)
											y(m)
											vx(m/s)
											vy(m/s)
											v(m/s)

3 ـ باختيار سلم رسم مناسب مثل أشعة السرعة في المواضع M₁، M₃، M₅، M₇،  M₉ ؟
4 ـ أوجد قيم شعاع تغير السرعة عند المواضع M₄، M₆، M₈ ؟ ماذا تلاحظ ؟
5 ـ مثل على ورقة ملمترية بيان تغير سرعة الكرة بدلالة الزمن ؟
6 ـ استنتج سرعة الكرة عند الموضعين M₀، M₁₀ ؟
7 ـ انطلاقا من الجدول بين طبيعة الحركة بين الموضعين (M₀، M₃ )، (M₃، M₁₀ )؟
8 ـ استنتج طبيعة الحركة على كل محور؟
9 ـ هل الكرة تخضع لقوة خلال حركتها ؟ اذا كان الجواب بنعم. أذكر خصائصها، ومثلها في نقاط كيفية ؟
10 ـ عرف مدى القذف، ثم أوجد قيمته، وأذكر العوامل المؤثرة فيه ؟
11 ـ دراسة حركة قذيفة (ع م 04)

الاجابة:

1 ـ المسار منحني.

2 ـ اتمام الجدول:

M10	M9	M8	M7	M6	M5	M4	M3	M2	M1	M0	المواضع
2,0	1,8	1,6	1,4	1,2	1,0	0,8	0,6	0,4	0,2	0	t(s)
0,60	0,54	0,48	0,42	0,36	0,30	0,24	0,18	0,12	0,06	0	x(m)
0,72	0,53	0,37	0,23	0,12	0,06	0,02	0	0	0	0	y(m)
0,3	0,3	0,3	0,3	0,3	0,3	0,3	0,3	0,3	0,3	/	vx(m/s)
/	0,88	0,75	0,62	0,42	0,25	0,15	0,05	0	0	/	vy(m/s)
/	0,93	0,81	0,69	0,52	0,39	0,33	0,3	0,3	0,3	/	v(m/s)

3 ـ تمثيل أشعة السرعة في المواضع M₁، M₃، M₅، M₇،  M₉:

لدينا:

 v₁ = 0,30 m.s^-1 ، v₃ = 0,30 m.s^-1 ، v₅ = 0,39 m.s^-1 ، v₇ = 0,69 m.s^-1 ، v₉ = 0,93 m.s^-1

نأخذ مقياس الرسم: 1 cm → 0,3 m.s^-1

ومنه:

v₁ → 1 cm ، v₃ → 1 cm  ، v₅ → 1,3 cm ، v₇ → 2,3 cm ،  v₉ → 3,1 cm

4 ـ ايجاد قيم شعاع تغير السرعة عند المواضع M₄ ، M₆ ، M₈:
يمكن ايجاد قيم شعاع تغير السرعة عند المواضع M₄ ، M₆ ، M₈  بالاعتماد على الانشاء الهندسي للأشعة كما يلي:

الملاحظة:

نلاحظ أن أشعة تغير السرعة لها نفس الجهة ونفس القيمة Δv₄ = Δv₆ = Δv₈

5 ـ تمثيل بيان تغير سرعة الكرة بدلالة الزمن:

لدينا جدول القيم:

M10	M9	M8	M7	M6	M5	M4	M3	M2	M1	M0	الموضع
2,0	1,8	1,6	1,4	1,2	1,0	0,8	0,6	0,4	0,2	0	t(s)
/	0,93	0,81	0,69	0,52	0,39	0,33	0,3	0,3	0,3	/	v(m/s)

6 ـ استنتاج سرعة العربة عند الموضعين M₀ ، M₁₀:

عند تمديد الخط البياني نجد أن:

v₀ = 0,3 m.s^-1 ، v₁₀ = 1,05 m.s^-1

7 ـ استنتاج طبيعة الحركة بين الموضعين (M₀ ، M₃ ) ، (M₃ ، M₁₀ ):

* بين الموضعين (M₀ ، M₃ ):

حركة الكرة مستقيمة منتظمة 

* بين الموضعين (M₃ ، M₁₀ ):

حركة الكرة منحنية متسارعة بانتظام 
8 ـ استنتاج طبيعة الحركة على كل محور:

ـ على المحور (OX) الحركة مستقيمة منتظمة لأن Δv = 0

ـ على المحور (OY)، نميز حالتين:

بين الموضعين (M₀ ، M₃ ): الكرة تعتبر ساكنة.

بين الموضعين (M₃ ، M₁₀ ):  حركة الكرة مستقيمة متسارعة بانتظام، لأن شعاع تغير السرعة في جهة الحركة، وقيمته ثابتة.  

9 ـ بين الموضعين (M₀ ، M₃ ): مجموع القوى المؤثرة على الكرة معدوم
   أما بين الموضعين (M₃ ، M₁₀ ): الكرة تخضع لقوة خلال حركتها، خصائصها من خصائص شعاع تغير السرعة، أي أن الكرة تخضع خلال حركتها لقوة ثابتة شاقولية نحو الأسفل، تسمى قوة الثقل، ونرمز لها بالرمز \(\vec{P}\)
تمثيل شعاع القوة:

10 ـ تعريف مدى القذف، وايجاد قيمته، وذكر العوامل المؤثرة فيه:

مدى القذف: هو البعد الأفقي الذي يفصل موضع القذف عن موضع السقوط على الأرض.

ايجاد قيمة المدى:

طريقة 1:

لدينا: 0,8 cm → 6 cm ومنه 5,6 cm → x cm أي مدى القذف x = 42 cm

طريقة 2:

لدينا على المحور (OX) الحركة مستقيمة منتظمة ومنه: x = v_x.t

ولدينا من الجدول السابق: v_x = 0,3 m.s^-1 ،  t = 7τ = 1,4 s

ومنه: x = 0,3×1,4 = 0,42 m   ومنه: x = 42 cm

العوامل المؤثرة في المدى:

يتغير المدى بتغير: - سرعة القذف v₀   

                        - زاوية القذف

III ـ دراسة حركة دائرية منتظمة:

نشاط 

للتأكد تجريبيا من خصائص القوة في الحركة الدائرية المنتظمة، نقوم بتسجيل الحركة التالية:
 ـ نستعمل "جسما محمولا ذاتيا"، وهو قرص تحتوي قاعدته السفلية ثقوبا صغيرة، ويبث فيه هواء مضغوط من الأعلى، بحيث خروج الهواء المضغوط من الأسفل، يكون "وسادة هوائية" بينه وبين الطاولة الأفقية التي تحمله، ذلك ما يسمح له بالتحرك دون احتكاك عليها.
ـ نشد القرص بخيط رفيع عديم الامتطاط طوله L إلى نقطة O، ثم نقذفه بمسطرة.
   يرفق القرص والطاولة بتجهيز يترك آثار مواضع القرص على ورقة خلال فترات زمنية متساوية.
ـ نعطي في الشكل الآتي تسجيلا لآثار مركز القرص M خلال حركته. 

حيث أن المدة الزمنية الفاصلة بين التقاطين متتاليين هي τ = 40 ms.

اعتمادا على هذا التسجيل:
1 ـ ماهي طبيعة مسار النقطة M ؟
2 ـ أوجد سرعة القرص عند المواضع M₁ ، M₂ ، M₃ ، M₄ ، M₅ ، M₆ ؟
3 ـ باختيار سلم رسم مناسب مثل أشعة السرعة في المواضع M₁ ، M₃ ، M₅ ؟
4 ـ أوجد قيمتي شعاعي تغير السرعة عند الموضعين M₂ ، M₄ ؟ ماذا تلاحظ ؟
5 ـ مثل على ورقة ملمترية بيان تغيرات سرعة القرص بدلالة الزمن ؟
6 ـ استنتج سرعة القرص عند الموضعين M₀ ، M₇ ؟
7 ـ استنتج طبيعة حركة القرص؟
8 ـ هل القرص خاضع لقوة خلال حركته ؟ اذا كان الجواب بنعم. أذكر خصائصها، ومثلها في نقاط كيفية ؟

الاجابة:

1 ـ المسار دائري.

2 ـ ايجاد سرعة القرص عند المواضع M₁ ، M₂ ، M₃ ، M₄ ، M₅ ، M₆ :

لدينا:

$$v_1 = v_2 = \frac{M_0 M_2}{2 \tau}$$

ومنه:

$$v_1 = \frac{10 \times 10^{-2}}{80 \times 10^{-3}}$$

ومنه:

v₁ = 1,25 m.s^-1

ولدينا:

$$v_2 = v_3 = \frac{M_1 M_3}{2 \tau}$$

ومنه:

$$v_2 = \frac{10 \times 10^{-2}}{80 \times 10^{-3}}$$

ومنه:

v₂ = 1,25 m.s^-1

و لدينا:

$$v_3 = v_4 = \frac{M_2 M_4}{2 \tau}$$

ومنه:

$$v_3 = \frac{10 \times 10^{-2}}{80 \times 10^{-3}}$$

ومنه:

v₃ = 1,25 m.s^-1

بنفس الطريقة نجد:

v₄ = 1,25 m.s^-1 ، v₅ = 1,25 m.s^-1 ، v₆ = 1,25 m.s^-1

3 ـ تمثيل أشعة السرعة في المواضع M₁ ، M₃ ، M₅ :

نأخذ مقياس الرسم 1,25 m.s^-1 → 1,2 cm

4 ـ ايجاد قيمتي شعاعي تغير السرعة عند الموضعين M₂ ، M₄ :

يمكن ايجاد قيمتي شعاعي تغير السرعة عند الموضعين M₂ ، M₄ بالاعتماد على الانشاء الهندسي للأشعة كما يلي:

الملاحظة:

نلاحظ أن أشعة تغير السرعة متجهة نحو مركز الدائرة، ومتساوية في الشدة.
لدينا جدول القيم:
5 ـ تمثيل بيان تغيرات سرعة القرص بدلالة الزمن:

M7	M6	M5	M4	M3	M2	M1	M0	الموضع
280	240	200	160	120	80	40	0	t(ms)
/	1,25	1,25	1,25	1,25	1,25	1,25	/	v(m.s-1)

6 ـ استنتاج سرعة القرص عند الموضعين M₀ ، M₇ :

عند تمديد الخط البياني نجد أن:

v₀ = 1,25 m.s^-1 ،  v₇ = 1,25 m.s^-1

7 ـ استنتاج طبيعة حركة القرص:

حركة القرص دائرية منتظمة، لأن أشعة تغير السرعة متساوية في القيمة، ومتجهة نحو مركز الدائرة (المسار).  

8 ـ نعم القرص يخضع لقوة خلال حركته ، خصائصها من خصائص شعاع تغير السرعة أي أن القرص يخضع خلال حركته لقوة \(\vec{F}\) ثابتة الشدة ومتجهة نحو مركز المسار في كل لحظة

تمثيل شعاع القوة:

IV ـ تطبيق: حركة الاقمار الاصطناعية:

يمكن اعطاؤه على شكل بحث، أو تلخيصه من الكتاب المدرسي.

وثيقة التلميذ بصيغة الـ PDF