الظواهر الكهربائية. دراسة ثنائي القطب RC

ملاحظة: توجد وثيقة التلميذ بصيغة الـ PDF في نهاية المقال.

III ـ دراسة ثنائي القطب RC:

1 ـ دراسة دارة الشحن:

نشاط ـ 8 ـ

نقوم بإتمام البيانات على التركيب:

ـ أكتب قانون جمع التوترات مع التذكير بعبارة قانون أوم ؟

لدينا: E - u_C – u_R = 0 ومنه: E = u_C + u_R

قانون أوم: u_R = R.i

ومنه: u_C + R.i = E 

ـ عبر عن i بدلالة u_C ؟

لدينا:

$$i = \frac{dq}{dt}$$

ومن جهة أخرى:

$$dq = C \, d u_C$$

بالتعويض:

$$i=C\frac{d{u}_C}{dt}$$

ـ بين أن:

$$\frac{du_C}{dt} + \frac{u_C(t)}{RC} - \frac{E}{RC} = 0$$

نبدأ من العلاقة الأساسية للدارة:

$$u_C + R \cdot i = E$$

وبما أن:

$$i = C \frac{du_C}{dt}$$

نستبدل $i$ في المعادلة:

$$u_C + R \cdot C \frac{du_C}{dt} = E$$

نرتب المعادلة:

$$R \cdot C \frac{du_C}{dt} + u_C - E = 0$$

نقسم طرفي المعادلة على $R \cdot C$ نجد:

$$\frac{du_C}{dt} + \frac{u_C}{RC} - \frac{E}{RC} = 0$$

وهذا يثبت المطلوب.

ـ ماهي عبارة ثابت الزمن τ ؟

τ = RC

ـ بين أن:

$$u_C(t) = E(1 - e^{-\frac{t}{\tau}})$$

هو حل للمعادلة التفاضلية:

$$\frac{du_C}{dt} + \frac{u_C(t)}{\tau} - \frac{E}{\tau} = 0 \tag{1}$$

الخطوات:

1. المعادلة المعطاة:

$$u_C(t) = E(1 - e^{-\frac{t}{\tau}}) \tag{2}$$

2. حساب المشتقة $\frac{du_C}{dt}$:
   

$$\frac{d{u}_C}{dt}=\frac{d}{dt}[E(1-e^{-\frac{t}{\tau }})]=E\cdot \frac{d}{dt}(-e^{-\frac{t}{\tau }})$$$$\frac{du_C}{dt} = E \cdot \frac{1}{\tau} e^{-\frac{t}{\tau}} \tag{3}$$

3. التعويض في المعادلة التفاضلية (1):
   نعوض $u_C(t)$ من (2) و $\frac{du_C}{dt}$ من (3) في (1):

$$\frac{du_C}{dt} + \frac{u_C(t)}{\tau} - \frac{E}{\tau} = 0$$$$\frac{E}{\tau} e^{-\frac{t}{\tau}} + \frac{1}{\tau} \cdot E(1 - e^{-\frac{t}{\tau}}) - \frac{E}{\tau} = 0$$

4. تبسيط العبارة:
   

$$\frac{E}{\tau} e^{-\frac{t}{\tau}} + \frac{E}{\tau} - \frac{E}{\tau} e^{-\frac{t}{\tau}} - \frac{E}{\tau} = 0$$

نبسط الحدود المشتركة:

$$\frac{E}{\tau} e^{-\frac{t}{\tau}} - \frac{E}{\tau} e^{-\frac{t}{\tau}} + \frac{E}{\tau} - \frac{E}{\tau} = 0$$$$0 = 0$$

5. النتيجة:
   المعادلة متحققة، وبالتالي:

$$u_C(t) = E(1 - e^{-\frac{t}{\tau}})$$

هو حل للمعادلة التفاضلية (1).

ـ أرسم بيان الدالة u_C(t) = E(1- e^-t/τ) ؟  

من أجل t = 0 نجد: u_C(0) = 0

ومن أجل t = τ نجد: u_C(τ) = 0,63E

ومن أجل t = 5τ نجد: u_C(5τ) ≃  E

التحليل البعدي لـ τ:

ـ بين أن i(t) = I.e^-t/τ ثم أرسم البيان الممثل لتغيرات i(t) ؟  

الاثبات بأن i(t) = I.e^-t/τ:

لدينا:

$$i(t) = C \cdot \frac{du_C}{dt}$$

ولدينا:

$$u_C(t) = E \left( 1 - e^{-\frac{t}{\tau}} \right)$$

إذن:

$$\frac{du_C}{dt} = \frac{E \cdot e^{-\frac{t}{\tau}}}{\tau}$$

وبما أن:

$$\tau = RC$$

فإن:

$$\frac{du_C}{dt} = \frac{E \cdot e^{-\frac{t}{\tau}}}{RC}$$

وبالتالي:

$$C \cdot \frac{du_C}{dt} = \frac{C \cdot E \cdot e^{-\frac{t}{\tau}}}{RC}$$

إذن:

$$i(t) = \frac{E \cdot e^{-\frac{t}{\tau}}}{R}$$

وبما أن:

$$\frac{E}{R} = I$$

فإن:

$$i(t) = I \cdot e^{-\frac{t}{\tau}}$$

رسم بيان الدالة i(t) = I.e^-t/τ:

من أجل t = 0 نجد: i(0) = I

ومن أجل τt =  نجد: i(τ) = 0,37I

ومن أجل t = 5τ نجد:  i(5τ) ≃ 0

ـ كيف يمكن استنتاج ثابت الزمن ؟

كيفية استنتاج ثابت الزمن:

من أجل ايجاد ثابت الزمن نعتمد على عدة طرق منها:

الطريقة الحسابية:

نطبق العلاقة  τ = RC

الطريقة الحسابية البيانية:

بالاعتماد على بيان الدالة u_C(t) = E(1 – e^-t/τ) نحسب المقدار 0,63E ثم نقوم بتمثيله على محور التراتيب ثم نسقط على البيان ثم نسقط على محور الزمن فنجد τ أنظر بيان الدالة u_C(t) = E(1 – e^-t/τ)

بالاعتماد على بيان الدالة i(t) = I.e^-t/τ نحسب المقدار 0,37I  ثم نقوم بتمثيله على محور التراتيب ثم نسقط على البيان ثم نسقط على محور الزمن فنجد τ أنظر بيان الدالة  i(t) = I.e^-t/τ

الطريقة البيانية:

بالاعتماد على بيان الدالة u_C(t) = E(1 – e^-t/τ)

نرسم المماس للبيان عند O(0 ; 0) فنجد أنه يقطع المستقيم المقارب u = E في النقطة d، نسقط النقطة d على محور الزمن فنجد τ 

أنظر بيان الدالة  u_C(t) = E(1 – e^-t/RC)

بالاعتماد على بيان الدالة i(t) = I.e^-t/τ

نرسم المماس للبيان عند (M(0 ; I  فنجد أنه يقطع محور الزمن عند τ، أنظر بيان الدالة i(t) = I.e^-t/τ

2 ـ دراسة دارة التفريغ :

نشاط ـ 9 ـ

نغلق القاطعة في الوضع (2)

ـ أكتب قانون جمع التوترات ؟  

عند غلق القاطعة في الوضع (2) يصبح المولد خارج الدارة ومنه نضع E = 0 ومنه نجد: 

u_C + u_R = 0

بين ان:

$$\frac{d u_C}{dt} + \frac{u_C(t)}{RC} = 0$$

لدينا:

$$u_C + u_R = 0$$

وبالتعويض عن $u_R$ باستخدام $u_R = R \cdot i$، نحصل على:

$$u_C + R \cdot i = 0$$

بما أن التيار $i$ يمكن التعبير عنه كالتالي:

$$i = C \cdot \frac{d u_C}{dt}$$

فإن المعادلة تصبح:

$$u_C + R \cdot C \cdot \frac{d u_C}{dt} = 0$$

بقسمة طرفي المعادلة على $RC$ وترتيبها، نحصل على:

$$\frac{d u_C}{dt} + \frac{u_C(t)}{RC} = 0$$

إذا أضفنا القوة المحركة الكهربائية للمولد $E$، فإن المعادلة تصبح:

$$\frac{d u_C}{dt} + \frac{u_C(t)}{RC} - \frac{E}{RC} = 0$$

وعند وضع $E = 0$، تعود المعادلة إلى شكلها الأساسي:

$$\frac{d u_C}{dt} + \frac{u_C(t)}{RC} = 0$$

ـ بين أن u_C(t) = E e^-t/RC  حل للمعادلة التفاضلية السابقة ؟

لدينا:

$$\frac{d u_C}{dt} + \frac{u_C(t)}{RC} = 0 \tag{1}$$

و لدينا:

$$u_C(t) = E e^{-t / RC}$$

بالاشتقاق نجد:

$$\frac{d u_C}{dt} = - \frac{E e^{-t / RC}}{RC} \tag{2}$$

بالتعويض في (1)، نحصل على:

$$- \frac{E e^{-t / RC}}{RC} + \frac{E e^{-t / RC}}{RC} = 0$$

وبالتالي، تتبسط المعادلة إلى:

$$0 = 0$$

وهذا يعني أن:

$$u_C(t) = E e^{-t / RC}$$

هو حل للمعادلة التفاضلية:

$$\frac{d{u}_C}{dt}+\frac{u_C(t)}{RC}=0$$

ـ أرسم بيان الدالة u_C(t) = E e^-t/RC ؟

من أجل t = 0 نجد: u_C(0) = E

ومن أجل t = τ نجد: u_C(τ) = 0,37E

ومن أجل t = 5τ نجد: u_C(5τ) ≃ 0

ـ بين أن i(t) = - I.e^-t/τ  ثم أرسم البيان الممثل لتغيرات i(t) ؟

الاثبات بأن i(t) = -I.e^-t/τ :

لدينا:

$$i = C \cdot \frac{d u_C}{dt}$$

ولدينا:

$$u_C(t) = E e^{-t / \tau}$$

وبالتالي نجد:

$$\frac{d u_C}{dt} = - \frac{E e^{-t / \tau}}{\tau}$$

ونعلم أن:

$$\tau = RC$$

لذا تصبح:

$$\frac{d u_C}{dt} = - \frac{E e^{-t / \tau}}{RC}$$

وبالتعويض في المعادلة $i = C \cdot \frac{d u_C}{dt}$:

$$C \cdot \frac{d u_C}{dt} = - C \cdot \frac{E e^{-t / \tau}}{RC}$$

وبالتالي نجد:

$$i(t) = - \frac{C E e^{-t / \tau}}{RC}$$

وهذا يبسط إلى:

$$i(t) = - \frac{E e^{-t / \tau}}{R}$$

وبما أن $\frac{E}{R} = I$، فإن المعادلة تصبح:

$$i(t)=-I{e}^{-t\mathrm{/}\tau }$$

رسم بيان الدالة i(t) = -I.e^-t/τ:

من أجل t = 0 نجد: i(0) = - I

ومن أجل t = τ نجد: i(τ) = - 0,37I

ومن أجل t = 5τ نجد: i(5τ) ≃ 0 

ـ كيف يمكن استنتاج ثابت الزمن ؟

يمكن استنتاج ثابت الزمن بنفس الطرق السابقة.

شحن مكثفة:

الوسائل المخبرية:

ـ مولد للتيار الثابت  E = 8,5 V .      ـ مقاومة  R = 10 KΩ . ـ مكثفة سعتها    C = 2200 μF .      ـ مقياس فولط متر . ـ مقياس أمبير متر .                        ـ أسلاك توصيل ، ميقاتية ، بادلة

التجربة:

1 ـ نحقق الدارة الكهربائية التالية بوضع البادلة في الوضع 1:

2 ـ نأخذ قيم التوتر بين طرفي المكثفة u_C خلال لحظات زمنية مختلفة ونسجل النتائج في الجدول التالي:

17	12	8	4	2	0	t(s)
4,5	3,5	2,5	1,5	1,0	0	uC(V)
120	78	54	43	35	25	t(s)
8,2	8,0	7,5	7,0	6,5	5,5	uC(V)

3 ـ باختيار سلم مناسب مثل بيانيا التابع: u_C = f(t)، ماذا تستنتج ؟

رسم بيان الدالة: u_C = f(t)

من البيان نستنتج أنه خلال عملية شحن المكثفة يتزايد فرق الكمون بين طرفيها وفق دالة أسية 

4 ـ أوجد قيمة الزمن المميز τ لشحن هذه المكثفة ؟

من البيان نجد: τ = 20 s

5 ـ باستعمال نفس التركيب السابق نأخذ قيم شدة التيار i المار في الدارة خلال لحظات زمنية مختلفة وندون النتائج في الجدول التالي:

18	10	8	4	2	0	t(s)
0,40	0,55	0,62	0,72	0,78	0,85	i(mA)
120	80	70	45	35	25	t(s)
0,05	0,07	0,08	0,15	0,22	0,31	i(mA)

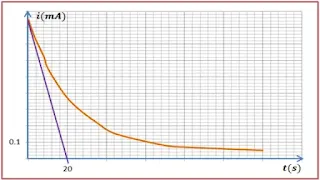
6 ـ مثل البيان i = f(t) ؟

رسم بيان الدالة: i = f(t)

7 ـ ماذا تلاحظ من البيان ؟

من البيان نلاحظ أن شدة التيار بين طرفي المكثفة تتناقص وفق دالة أسية خلال عملية الشحن 

8 ـ أ / أكتب عبارة  u_R(t) ثم أملا الجدول التالي: 

كتابة عبارة u_R(t):

لدينا: u_R(t) = R.i(t) ولدينا:

R = 10 KΩ = 10⁴ Ω

ومنه:  

u_R(t) = 10⁴.i(t)

t(s)	0	2	4	8	10	18
uR(V)	8,5	7,8	7,2	6,2	5,5	4,0
t(s)	25	35	45	70	80	120
uR(V)	3,1	2,2	1,5	0,8	0,7	0,5

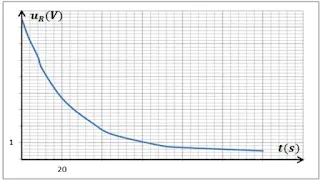
ب ـ مثل المنحنى: u_R = g(t) ، ماذا تستنتج ؟

رسم بيان الدالة: u_R = g(t)

من البيان نستنتج أنه خلال عملية شحن المكثفة يتناقص فرق الكمون بين طرفي الناقل الأومي وفق دالة أسية

تفريغ مكثفة:

التجربة:

1 ـ نحقق الدارة الكهربائية التالية بوضع البادلة في الوضع 2:

2 ـ نسجل قيم التوتر u_C بين طرفي المكثفة، والزمن الموافق لذلك، ثم ندون النتائج في الجدول التالي:   

16	11	7	4	2	1	0	t(s)
4.0	5.0	6.0	7.0	7.5	8.0	8.5	uC(V)
75	65	49	39	33	27	19	t(s)
0.5	0.5	1.0	1.5	2.0	2.5	3.5	uC(V)

3 ـ مثل البيان (u_C = f(t  ـ ماذا تستنتج ؟

رسم بيان الدالة: (u_C = f(t

من البيان نستنتج أنه خلال عملية تفريغ المكثفة يتناقص فرق الكمون بين طرفيها وفق دالة أسية

4 ـ نسجل قيم شدة التيار i(t والزمن الموافق لكل قراءة ثم ندون النتائج في الجدول التالي:

18	14	10	6	4	2	0	t(s)
-0,35	-0,42	-0,50	-0,60	-0,65	-0,72	-0,85	i(mA)
110	100	90	70	50	35	25	t(s)
0	0	-0.01	-0,03	-0,08	-0, 16	-0,26	i(mA)

5 ـ مثل المنحنى i = f(t) ، ماذا تلاحظ ؟

رسم بيان الدالة: i = f(t)

من البيان نستنتج أنه خلال عملية تفريغ المكثفة تتزايد شدة التيار المار في الدارة وفق دالة أسية من قيمة أعظمية سالبة حتى تنعدم

6 ـ استنتج تغيرات التوتر u_R(t) بين طرفي الناقل الأومي بدلالة الزمن t ثم مثل المنحنى u_R = g(t) ؟

كتابة عبارة  u_R(t):

لدينا: u_R(t) = R.i(t) ولدينا:

R = 10 KΩ = 10⁴ Ω

ومنه:

u_R(t) = 10⁴.i(t)

t(s)	0	2	4	6	10	14	18
uR(V)	-8,5	-7,2	-6,5	-6,0	-5,0	-4,2	-3,5
t(s)	25	35	50	70	90	100	110
uR(V)	-2,6	-1,6	-0,8	-0,3	-0,1	0	0

7 ـ من المنحنى السابق حدد ثابت الزمن τ بيانيا ؟

بحساب القيمة  0,37(u_R)_max وتمثيلها على محور التراتيب والاسقاط على البيان ثم الاسقاط على محور الزمن نجد :

 τ = 20 s

3 ـ الطاقة المخزنة في مكثفة:

ـ إيجاد عبارة الطاقة:

نشاط ـ 1 ـ

عند رسم بيان الدالة q = f(u) نجد انه يأخذ الشكل التالي:

إذا علمت أن قيمة الطاقة المخزنة في المكثفة تساوي مساحة المثلث ADB

ـ أوجد عبارة هذه الطاقة بدلالة:

أ ـ q ، u ؟  

  عبارة الطاقة المخزنة في المكثفة بدلالة q ، u:

$$E_{(C)} = \frac{1}{2} q \cdot u_C$$

ب ـ u ، C  ؟    

 عبارة الطاقة المخزنة في المكثفة بدلالة u ، C:

$$E_{(C)} = \frac{1}{2} C \cdot u_C^2$$

جـ ـ q ، C ؟

عبارة الطاقة المخزنة في المكثفة بدلالة q ، C:

$$E_{(C)} = \frac{q^2}{2C}$$

إيجاد زمن تناقص الطاقة المخزنة في المكثفة إلى النصف (t_1/2)

بالاعتماد على المعلومات السابقة.

1 ـ أوجد عبارة E_(C) عند  t = 0 ، t = t_1/2 ؟

لدينا: E_(C) = ½C.u_C² → (1)

ولدينا: ^τu_C(t) = E e^-t/

ومنه: (u_C(t))² = E² e^-2t/τ → (2)

بتعويض (2) في (1) نجد:

E_(C) = ½C.E².e^-2t/τ

عند  t = 0نجد:

E_(C)(0) = ½C.E² 

وعند t = t_1/2 نجد:

E_(C)(t_1/2) = ½C.E².e^-2t1/2/τ → (3)

ولدينا كذلك

E_(C)(t_1/2) =½.½.C.E²  → (4)

2 ـ بين أن t_1/2 = (τln2)/2 ؟

من العلاقتين (3) و (4) نجد:C.E².e^-2t1/2/τ =½C.E² 

ومنه: e^-2t1/2/τ=1/2  ومنه: lne^-2t1/2/τ=ln(1/2)

ومنه: - 2t_1/2/τ = - ln2  ومنه:  t_1/2 = (τln2)/2

وثيقة التلميذ بصيغة الـ PDF