بكالوريا تجريبية في مادة الفيزياء، ماي 2025. م2(ر+ ت ر)

الموضوع الثاني

ملاحظة: يوجد الموضوع مع الحل بصيغة الـ PDF في نهاية المقال.

الجزء الأول: يتكون من ثلاثة تمارين.

التمرين الأول: (04.00 نقاط)

نفذ غاليلي تجاربه على المستوى المائل، ليتحقق من فرضيته التي تنص على أن، جميع الأجسام تسقط بنفس التسارع، مهما كانت كتلتها، أكمل تلك النتائج التي حصل عليها غاليلي. العمل الذي قام به علماء آخرون مثل یوهانس كيبلر، وساهمت في وضع قوانين الميكانيك، التي صاغها إسحاق نيوتن لاحقا، كما يعتبر غاليلي أول من فكر في مبدأ انحفاظ الطاقة عام 1638، ثم جاء بعده علماء آخرون مثل جوتفريد لايبنتز خلال الأعوام 1676-1689، وقاموا بصياغة مبدأ الحفاظ الطاقة، ......

I- دراسة حركة جسم على مستوى مائل، وقذفه في الهواء:

يضغط نابض مرن حلقاته غير متلاصقة، ثابت مرونته K من B إلى A بالمقدار: X₀ = AB = 6cm ، بواسطة كرية (S) كتلتها  m = 100gغير مثبتة به، ثم نتركها لحالها دون سرعة ابتدائية.

عند اللحظة t = 0s تنفصل الكرية (S) عن النابض، عند الوضع B بسرعة ابتدائية v₀ = v_B، لتواصل حركتها على سطح خشن BC مائل (α = 30°). (الشكل -01-)

1 ـ مثل الحصيلة الطاقوية للجملة (كرية + نابض) بين الوضعين A وB.

2 ـ بتطبيق مبدأ انحفاظ الطاقة، أوجد عبارة v₀ سرعة الكرية (S) عند B ، بدلالة المقادير التالية: α، g، m، X₀.

3- سمح تجهيز مناسب بقياس سرعة الكرية (S) في مواضع مختلفة على الجزء BC ، ورسم البيان v² = f(x)

أ ـ بتطبيق القانون الثاني لنيوتن على مركز عطالة الكرية (S) ، أوجد عبارة تسارع مركز عطالتها.

ب ـ بين أن سرعة الكرية (S) عند أي لحظة t أثناء الانتقال على الجزء BC ، تعطى بالعلاقة: v² = 2a.x + v₀²

جـ - باستغلال البيان والعلاقة السابقة، أحسب شدة قوة الاحتكاك f، وثابت مرونة النابضK

4 - أ- بإهمال تأثير الهواء على حركة الكرية (S) بعد مغادرتها النقطة C:

- بين أن معادلة مسارها في المعلم $((CX) ⃗, (CY) ⃗)$ تُعطى بالعلاقة:

$$y(x) = \frac{g}{2v_0^2 \cos^2\alpha} \cdot x^2 + x \cdot \tan\alpha$$

ب- أحسب قيمة سرعة الكرية (S) لحظة اصطدامها بالأرض في النقطة M، علما أنها ترتفع عن المستوي

الأفقي المار بالنقطة C بـ 40 cm.

II ـ دراسة حركة نواس مرن:

في الجملة السابقة نثبت نهاية النابض المرن المائل مع الكرية، ونهمل كل الاحتكاكات على المستوي المائل، ثم نزيح الجملة (كرية - نابض) عن وضع توازنها، في اتجاه تمدد النابض بـ 4cm ، ونتركها لحالها دون سرعة ابتدائية في اللحظة t = 0

1 ـ مثل القوى المؤثرة على مركز عطالة الكرية في موضع فاصلته x(t).

2- أوجد المعادلة التفاضلية للحركة بدلالة مطالها x(t) ، وأعط حلا لها.

3- استنتج العبارة الحرفية للدور الذاتي للحركة.

4- علما أن سرعة مركز عطالة الكرية عند المرور بوضع التوازن: v = 0,55m/s

استنتج: أ- الدور الذاتي للحركة و تواترها.

ب ـ ثابت مرونة النابض (K)، وقارنه بالقيمة السابقة.

التمرين الثاني: (04.00 نقاط)

هل تساءلت يوماً كيف لنواة صغيرة غير مستقرة أن تغير مجرى الطبيعة، أو تشغل محطة طاقة عملاقة؟ نعم هذا ما يحدث حقيقة، وما توصل إليه العلماء نظريا، وحقق تجريبيا، وتمت الاستفادة منه في مجالات عديدة، ومن الأمثلة والعناصر الشائعة اليورانيوم 238 المشع $\left(_{92}^{238}\text{U}\right)$، وهو عنصر مستقر. الذي يتفكك تلقائيا ببطء، لينتج عنه عناصر جديدة أكثر استقراراً، فدراسة سلسلة تفككاته تساعد على معرفة عمر الصخور، وعمر الأرض نفسها ...، وأيضا عنصر البلوتونيوم 241$\left(_{94}^{241}\text{Pu}\right) ،$الذي تعتبر استخداماته محدودة نظرا لقصر زمن نصف عمره، وعليه فنشاطه الإشعاعي يكون عالي جداً.

يهدف هذا التمرين لتحديد زمن نصف عمر اليورانيوم$\left(_{92}^{238}\text{U}\right)$، والتحقق من قيمة النشاط الإشعاعي العالي لعنصر البلوتونيوم $\left(_{94}^{241}\text{Pu}\right)$.

I ـ 1ـ مالمقصود بالمصطلحات الواردة في السياق السابق: زمن نصف العمر، عنصر مستقر، نشاط إشعاعي.

2- اليورانيوم$\left(_{92}^{238}\text{U}\right)$نظير مشع، يتفكك عبر عدة تفككات متتالية من نوع α وβ^-، إلى النظير المستقر من الرصاص $\left(_{82}^{206}\text{Pb}\right)$، وفق المعادلة النووية التالية: 

$$_{92}^{238}\text{U} \rightarrow _{82}^{206}\text{Pb} + x\alpha + y\beta^-$$

أ ـ بتطبيق قانونا الانحفاظ لصودي حدد قيمتي كل من x ، y .

ب ـ بين أن كتلة الرصاص الناتجة في اللحظة t تعطى بالعلاقة:

m_Pb(t) = 0,866.m₀(U)[1 – e^-λt]

حيث: m_Pb(t) كتلة الرصاص الناتجة في اللحظة t.

m₀(U) كتلة اليورانيوم 238 الابتدائية.

λ يمثل ثابت التفكك الإشعاعي لليورانيوم 238.

3- المنحنى الموضح بالشكل (3) المقابل يعطي تغيرات النسبة (t)γ

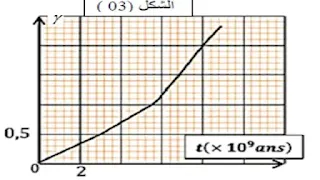
بين كتلة الرصاص الناتج وكتلة اليورانيوم المتبقي بدلالة الزمن حيث:

$$\gamma(t) = \frac{m_{\text{Pb}}(t)}{m_{\text{U}}(t)}$$

أ- أكتب عبارة النسبة (t)γ بدلالة λ ، t.

ب- باستعمال العلاقة السابقة والمنحنى البياني حدد قيمتي t_1/2 وλ.

II ـ إن قذف نواة اليورانيوم $^{238}_{92}\text{U}$ بنيترونات، يمر عبر عدة مراحل، وتفككات ليعطي دواة البلوتونيوم $^{241}_{94}\text{Pu}$، المشعة وفق المعادلة التالية:

$$^{238}_{92}\text{U} + x \cdot ^{1}_{0}\text{n} \rightarrow ^{241}_{94}\text{Pu} + y \cdot ^{0}_{-1}\text{e}$$

1ـ أوجد كل من x،  y. هل يصنف هذا التحول انشطاريا أم اندماجيا، أو لا يصنف ضمن كليهما؟ مع التعليل. 

2 ـ تتفكك نواة البلوتونيوم $^{241}_{94}\text{Pu}$ المشعة تلقائيا، لتعطي نواة الأمريكيوم $^{241}_{95}\text{Am}$ في حالة مثارة، ثم بعد ذلك تتخلص من الإثارة عن طريق تحرير إشعاع معين، أكتب معادلات التفكك المنمذج لهذا التحول النووي، محددا نمط التفكك وخصائصه.

3 ـ عينة من البلوتونيوم $^{241}_{94}\text{Pu}$ كتلتها $m_0 = 1\,\text{mg}$ عند اللحظة $t = 0$. بعد فترة تم قياس نشاطها الإشعاعي لحظتين مختلفتين حيث وجد:

$$\left\{ \begin{array}{l} t_1 = 3\,\text{ans} \quad \Rightarrow \quad A_1 = 3{,}4 \times 10^9\,\text{Bq} \\ t_2 = 5\,\text{ans} \quad \Rightarrow \quad A_2 = 3{,}08 \times 10^9\,\text{Bq} \end{array} \right.$$

* أحسب قيمة ثابت النشاط الإشعاعي λ، ثم قيمة النشاط الإشعاعي الإبتدائي للعينة A₀، ماذا تلاحظ فيما يخص قيمة النشاط الإشعاعي الإبتدائي للبلوتونيوم 241 ؟

معطيات:

$$\left\{ \begin{array}{l} M_U = 238\,\text{g/mol} \\ M_{Pb} = 206\,\text{g/mol} \end{array} \right.$$

التمرين الثالث: (06.00 نقاط)

تستعمل المكثفات، الوشائع، النواقل الأومية في الكثير من الأجهزة الكهربائية، وتختلف وظيفتها حسب طريقة ربطها، ويمكن استعمال الأعمدة الكهروكيميائية في الدارات المنجزة، وخاصة في المخابر التعليمية.

نستهدف في هذا التمرين إلى دراسة عمود كهربائي، واستخدامه في دراسة ثنائي القطب RL.

I ـ دراسة عمود كهروكيميائي:

يمثل الشكل (04) عمودا كهروكيميائيا حيث يعطى:

* تركيز محلول نترات الرصاص C₁ = 0,2 mol/L

* تركيز محلول نترات الفضة C₂ = 0,1mol/L

1 ـ أعط الرمز الإصطلاحي لهذا العمود.

2 ـ ماذا ينقص الشكل حتى يمر التيار في الناقل الأومي؟

- بين ذلك على الشكل مع تكملته، وتوضيح اتجاه الالكترونات التي تجتاز الناقل (إعادة رسم الشكل).

3- أكتب المعادلات النصفية الإلكترونية للتفاعلات التي تحدث عند المسرين، ومعادلة التفاعل أكسدة - إرجاع.

4- أحسب كسر التفاعل الابتدائي، وعين جهة التطور التلقائي للجملة.

5- نفرغ العمود في الناقل الأومي لمدة قدرها 2h ، ونقيس شدة التيار فنجد I = 50mA.

أ- أحسب كمية الكهرباء التي تمر في الدارة.

ب- عين التراكيز المولية للشوارد المعدنية في كل بيشر بعد هذه المدة من الاشتغال.

المعطيات: ثابت توازن الجملة: K = 6,8.10²⁸ ، حجم كل محلول: V = 200 mL، 1F = 96500 C.mol^-1

II- دراسة ثنائي القطب RL:

لأجل دراسة ثنائي القطب RL استعمل عدد من الأعمدة السابقة موصولة على التسلسل، قوتها المحركة الكهربائية المكافئة تساوي E، مع وشيعة مثالية ذاتيتها L ، وناقل أومي مقاومته R ، لاقط التوتر لجهاز EXAO.

نحقق الدارة الكهربائية المبينة بالشكل (05).

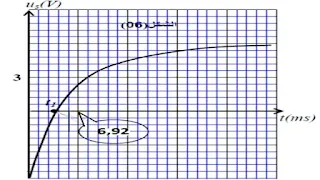
عند اللحظة t = 0 نغلق القاطعة K، ونتابع بواسطة لاقط التوتر لجهاز EXAO تطور التوتر u_s(t) =u_R – u_b(t)

الموضح في الشكل (06).

1 ـ أعد رسم الدارة مع توجيه شدة التيار والتوترات.

2 ـ بين أن المعادلة التفاضلية لـ u_s(t):

$$\frac{d u_s(t)}{dt} + \frac{1}{\tau} u_s(t) = \frac{E}{\tau}$$

3- يعطى حل المعادلة التفاضلية بـ : u_s(t) = A – C.e^-Bt

أوجد عبارة الثوابت A ، B ، C.

4 ـ بين أن البيان u_s(t) يقطع محور الأزمنة في اللحظة t₁ = τ.ln2.

5- اعتمادا على البيان أوجد قيمة كل من: E ، τ ، R .

الجزء الثاني: يتكون من تمرين واحد تجريبي.

التمرين التجريبي: (06.00 نقاط)

إن محلول روح الملح التجاري، يعد محلولاً مائياً لغاز كلور الهيدروجين (HCl)، وهو حمض معدني قوي، ويمثل المكون الأساسي لحمض المعدة، وقد اكتشفه جابر بن حيان في عام 800 م، ثم أصبح سلعة كيميائية مهمة في العديد من التطبيقات خلال فترة الثورة الصناعية، حيث استخدم في إنتاج العديد من المركبات العضوية، مثل كلوريد الفينيل، كما يستخدم في مجال الصناعة كصناعة البلاستيك، المطاط، وإزالة الصدأ من الحديد، ويجب التعامل معه بحذر شديد، کونه سائل شديد التآكل.

يهدف هذا التمرين إلى دراسة محلول حمض كلور الهيدروجين التجاري، والتأكد من خصائصه المدونة على قارورته.

قارورة تجارية لمحلول حمض كلور الهيدرجين، كتب عليها المعلومات التالية:

الصيغة الجزيئية: HCl النسبة المئوية الكتلية (نسبة النقاوة): P = 10,3% الكثافة: d = 1,068 الكتلة المولية الجزيئية: M = 36,5g.mol-1

للتحقق من النسبة المئوية الكتلية المحلول حمض كلور الهيدروجين التجاري، (روح الملح) المسجلة على القارورة التجارية (10,3%)، قسم أستاذ تلاميذه في حصة الأعمال المخبرية إلى ثلاثة أفواج، وكلف كل فوج بتجربة. من أجل ذلك قام كل فوج بتمديد المحلول التجاري (S₀) ، الذي تركيزه المولي (C₀) 200 مرة، فتحصلوا على محلول ممدد (S) تركيزه المولي (C_a).
I ـ تحضير محلول كلور الهيدروجين انطلاقا من محلول تجاري:

1 ـ من المعطيات السابقة الخاصة بالتحضير، أحسب قيمة التركيز المولي (C₀) للمحلول التجاري (S₀).

2 ـ قدم بروتوكولا تجريبيا لتحضير المحلول الممدد (S)، حجمه V = 200 ml، انطلاقا من المحول التجاري (S₀).

II ـ تجربة الفوج الأول: المعايرة اللونية لمحلول حمض كلور الهيدروجين المحضر.

قام التلاميذ بمعايرة حجم V_a = 20 mL، من المحلول (S) لحمض كلور الهيدروجين التجاري (H₃O⁺_(aq) + Cl^-_(aq)) بمحلول هيدروكسيد الصوديوم (Na⁺_(aq) + OH^-_(aq))، ذي التركيز المولي C_b = 0,1 mol/L، وتحصلوا على التكافؤ عند إضافة حجم V_bE = 3 mL.

1- أرسم التركيب التجريبي للمعايرة اللونية، موضحا عليه البيانات اللازمة.

2 ـ أكتب معادلة تفاعل المعايرة.

3 - أحسب التركيز المولي للمحلول الحمضي الممدد (C_a)، ثم استنتج التركيز المولي (C₀) للمحلول التجاري (S₀)

4 ـ أحسب النسبة المئوية الكتلية لحمض كلور الهيدروجين في المحلول التجاري (S₀) ( درجة النقاوة ).

III ـ تجربة الفوج الثاني: متابعة زمنية لتحول كيميائي تام بين كربونات الكالسيوم الصلبة (CaCO_3(s))، ومحلول حمض كلور الهيدروجين التجاري الممدد (H₃O⁺_(aq) + Cl^-_(aq)):

التحول الكيميائي التام بين كربونات الكالسيوم الصلبة (CaCO_3(s))، ومحلول حمض كلور الهيدروجين التجاري الممدد (H₃O⁺_(aq) + Cl^-_(aq))، ينمذج بمعادلة التفاعل التالية:

CaCO_3(s) + 2H₃O⁺_(aq) = Ca²⁺_(aq) + CO_2(g) + 3H₂O_(ℓ)

وضع التلاميذ في دورق حجما V = 60 mL من المحلول الحمضي التجاري الممدد (S)، تركيزه المولي (C_a)، وكتلة m₀ = 1g من كربونات الكالسيوم.

سمح تجهيز الشكل (07)، بقياس حجم غاز ثاني أكسيد الكربون المنطلق في الحالة النهائية V_f(CO₂) = 10 mL

1 ـ أكمل البيانات على التركيب التجريبي، ثم أنشئ جدولا لتقدم التفاعل.

2 ـ أحسب التركيز المولي للمحلول الحمضي الممدد (C_a)، ثم استنتج التركيز المولي (C₀) للمحلول التجاري (S₀).

3 ـ أحسب النسبة المئوية الكتلية لحمض كلور الهيدروجين في المحلول التجاري (S₀)(درجة النقاوة).

يعطى: ρ_eau=1000 g/L ، M(CaCO₃) = 100 g/mol ، V_M = 22,4 L/mol.

IV ـ تجربة الفوج الثالث: المعايرة عن طريق قياس الناقلية لمحلول حمض كلور الهيدروجين المحضر.

أخذ التلاميذ حجما V_a = 10 mL من محلول حمض كلور الهيدروجين التجاري الممدد (H₃O⁺_(aq) + Cl^-_(aq))، وتم معايرته بمحلول هيدروكسيد الصوديوم (Na⁺_(aq) + OH^-_(aq))، ذي التركيز المولي C_b = 0,01 mol/L، عن طريق قياس الناقلية النوعية (σ)، النتائج التجريبية المتحصل عليها سمحت بتمثيل البيان σ = f(V_b)، الموضح بالشكل (08).

1 ـ أكتب معادلة تفاعل المعايرة.

2 ـ حدد بيانيا قيمة حجم محلول هيدروكسيد الصوديوم اللازم للتكافؤ.

3 ـ جد بطريقتين مختلفتين التركيز المولي للمحلول الحمضي الممدد (C_a)، ثم استنتج التركيز المولي (C₀) للمحلول الحمضي التجاري (S₀).

4 ـ أحسب تراكيز مختلف الأفراد الكيميائية في المزيج عند التكافؤ، ثم استنتج اسم الملح الناتج وكتلته.

5 ـ أحسب النسبة المئوية الكتلية لحمض كلور الهيدروجين في المحلول التجاري (S₀) ( درجة النقاوة ).

6 ـ من التجارب الثلاث السابقة، ماهي النتيجة المستخلصة ؟

يعطى:

• $\lambda_{\mathrm{Na}^+} = 5 \ \mathrm{mS \cdot m^2 \cdot mol^{-1}}$
  

• $\lambda_{\mathrm{H_3O}^+} = 35 \ \mathrm{mS \cdot m^2 \cdot mol^{-1}}$
  

• $\lambda_{\mathrm{Cl}^-} = 7{,}6 \ \mathrm{mS \cdot m^2 \cdot mol^{-1}}$
  

ρ_eau = 1000 g/L ، M(Cl) = 35,5 g/mol ، M(Na) = 23 g/mol

تصحيح الموضوع الثاني

الجزء الأول: يتكون من ثلاثة تمارين.

تصحيح التمرين الأول: (04.00 نقاط)

I- دراسة حركة جسم على مستوى مائل، وقذفه في الهواء:

1- تمثيل الحصيلة الطاقوية للمجموعة (جسم + نابض) بين الموضعين $A$ و $B$ :

2- إيجاد عبارة سرعة الكرة عند B بدلالة المقادير:

$K, g, \alpha, X_0, m$

بتطبيق مبدأ انحفاظ الطاقة بين الموضعين $B$ و $A$ نجد:

$$E_{mA} + W_{\overrightarrow{P}}(A \rightarrow B) = E_{cB}$$$$\frac{1}{2}K(X_0)^2 + mgh = \frac{1}{2}mv_0^2 \quad /h = X_0 \sin \alpha$$ومنه:
$$\frac{1}{2}K(X_0)^2 + mgX_0 \sin \alpha = \frac{1}{2}mv_0^2$$ $$v_0 = \sqrt{\frac{K(X_0)^2}{m} + 2gX_0 \sin \alpha} \tag{01}$$

3- أ- ايجاد عبارة تسارع مركز عطالة الجسم:

بتطبيق القانون الثاني لنيوتن على مركز عطالة الكرة، نحصل على:

$$\overrightarrow{p} + \overrightarrow{R} + \overrightarrow{f} = m \overrightarrow{a}$$

بالإسقاط على محور الحركة نجد:

$$P_x - f = ma \quad \Rightarrow \quad mg \sin \alpha - f = ma$$ومنه:
$$\Rightarrow a = g \sin \alpha - \frac{f}{m} \tag{02}$$

ب- إثبات أن سرعة الجسم أثناء الانتقال على BC تعطى بالعلاقة:
$$v^2 = v_0^2 + 2a x$$

بتطبيق مبدأ انحفاظ الطاقة بين الموضعين B و C​ نجد:

$$E_{c_0} + W_{BC}(\vec{P}) - W_{BC}(\vec{f}) = E_{c_c}$$ $$\frac{1}{2}mv_0^2 + mgh - f \cdot BC = \frac{1}{2}mv^2$$$$\text{حيث} \quad h = BC \cdot \sin(\alpha)$$ومنه:
$$\frac{1}{2}mv_0^2 + mgBC \sin \alpha - f \cdot BC = \frac{1}{2}mv^2$$ومنه:
$$v^2 = 2gBC \sin \alpha - \frac{2f}{m} \cdot BC + v_0^2 \quad /a = \frac{f}{m}$$ $$v^2 = 2BC(g \sin \alpha - a) + v_0^2 \quad /BC = x$$ومنه:
$$\Rightarrow v^2 = 2ax + v_0^2 \tag{03}$$

جـ - حساب شدة قوة الاحتكاك $\overrightarrow{f}$و ثابت مرونة النابض $K$:

معادلة البيان:

$$v^2 = \alpha x + \beta \tag{04}$$

نظريا لدينا:

$$v^2 = 2a x + v_0^2 \tag{05}$$

بمطابقة (04) و (05) نجد:

$$\alpha = 2a \quad \Rightarrow \quad a = \frac{4}{2} = 2$$ومنه:
$$a = \frac{1m}{1s^2}$$ومنه:
$$\beta = v_0^2 = 2 \Rightarrow v_0 = \sqrt{2}\, m/s$$

حساب ثابت مرونة النابض $K$:

نستعمل العلاقة:

$$v_0 = \sqrt{ \frac{K X^2}{m} + 2g X \sin \alpha }$$

نستخرج $K$:

$$K = \frac{m}{X^2} \left( v_0^2 - 2gX \sin \alpha \right)$$

بالتعويض العددي:

$$K = \frac{0.1}{(0.08)^2} \left( 2 - 2 \times 10 \times 0.08 \times 0.5 \right)$$$$\Rightarrow K = 18.75 \, \text{N/m}$$

حساب قوة الاحتكاك $f$:

من العلاقة:

$$a = g \sin \alpha - \frac{f}{m} \Rightarrow f = m(g \sin \alpha - a)$$

بالتعويض العددي:

$$f = 0.1 (10 \times 0.5 - 1) \Rightarrow f = 0.4 \, \text{N}$$

4- أ ـ اثبات أن معادلة المسار في المعلم
$\overrightarrow{C_1 C_2}$ تعطى بالعلاقة:

$$y = x \tan \alpha - \frac{g x^2}{2 v_0^2 \cos^2 \alpha}$$

دراسة الحركة على المحورين:

من معادلة المسار:

$$t = \frac{x}{v_0 \cos \alpha}$$

• بالتعويض في y نجد:

$$y = -\frac{g}{2} \left( \frac{x}{v_0 \cos \alpha} \right)^2 + v_0 \sin \alpha \cdot \left( \frac{x}{v_0 \cos \alpha} \right)$$ومنه:
$$y = x \tan \alpha - \frac{g x^2}{2 v_0^2 \cos^2 \alpha}$$

وهي معادلة فرع من قطع مكافئ ومنه المسار منحني.

ب ـ حساب قيمة سرعة الجسم لحظة اصطدامه بالأرض في النقطة M :

         في البداية يجب حساب زمن السقوط من C حتى M فنجد:

$y = \frac{1}{2}gt^2 + v_c \sin \alpha t$

لدينا:

$$0{,}4 = 5t^2 + t$$

منه:

$$5t^2 + t - 0{,}4 = 0 \quad \rightarrow (03)$$

بعد الحل نجد : $t = 0,2s$

ثم نحسب قيمة مركبتي السرعة عند $M$ نجد :

$v_x = v_c = \sqrt{3} \, m/s$

$v_y = gt + v_c \sin \alpha = 10 \times 0,2 + 1 = 3 \, m/s$

لدينا:

$$v_M = \sqrt{v_x^2 + v_y^2}$$

وبالتعويض:

$$v_M = \sqrt{3 + 9} = \sqrt{12} \approx 3{,}46 \ \text{m/s}$$

II- دراسة حركة نواس مرن:

1- تمثيل القوى المؤثرة على مركز عطالة الكرية في موضع فاصلته x(t) :

2- ايجاد المعادلة التفاضلية للحركة بدلالة مطالها x(t) ، وحلها:

في البداية يجب ايجاد شرط التوازن فنجد:

$\sum \vec{F_x} = \vec{0}$

$\vec{P} + \vec{R} + \vec{T} = \vec{0}$

لدينا المعادلة الناتجة عن إسقاط القوى على المحور (Ox):

$$P_x - T = 0$$

وبما أن القوة $P$ تساوي وزن الجسم $mg$ ويشكّل زاوية $\alpha$ مع المحور الأفقي، نجد:

$$mg \cdot \sin(\alpha) - T = 0 \tag{01}$$

بتطبيق القانون الثاني لنيوتن على مركز عطالة الكرية نجد:

$\sum \vec{F_x} = m \vec{a}$

$\vec{P} + \vec{R} + \vec{T} = m \vec{a}$

بالإسقاط على المحور $ox$ نجد:

$P_x - T = ma \Rightarrow mg \sin \alpha - k.(x + \Delta l) = ma$

$\Rightarrow mg \sin \alpha - k.X - kx = ma$

$\Rightarrow -k.x = ma = \frac{d^2 x}{dt^2} + \frac{k}{m}x = 0 ..........(02)$

المعادلة (02) هي معادلة تفاضلية من الدرجة الثانية لحركة جيبية ، وبالتالي نقول أن الحركة اهتزازية جيبية دورية غير متخامدة.

حلها من الشكل:

$x(t) = X_0 \cos(\omega_0 t + \varphi) ..........(03)$

3- استنتاج العبارة الحرفية للدور الذاتي للحركة:

من المعادلة التفاضلية نجد:

$\omega_0^2 = \frac{k}{m}$

$\Rightarrow T_0 = \frac{2\pi}{\omega_0} = 2\pi \sqrt{\frac{m}{k}} ..........(04)$

4- علما أن سرعة مركز عطالة الكرة عند المرور بموضع التوازن: $v = 0,55 \, m/s$

أ- استنتاج الدور الذاتي للحركة وتواتره:

عند المرور بموضع التوازن تكون السرعة عظمى ومنه:

$$v = X_0 \cdot \omega_0$$

ومنه:

$$\omega_0 = \frac{v}{X_0} = \frac{0{,}55}{0{,}04} = 13{,}75 \ \text{rad/s}$$

ومن جهة أخرى، لدينا:

$$T_0 = \frac{2\pi}{\omega_0} = \frac{6{,}28}{13{,}75} \approx 0{,}46 \ \text{s}$$

ب- حساب ثابت مرونة النابض (k):

لدينا:

$$\omega_0^2 = \frac{k}{m}$$

ومنه:

$$k = m \cdot \omega_0^2$$

ومنه:

$$k = 0{,}1 \times (4{,}37)^2 = 18{,}8 \ \text{N/m}$$

* المقارنة: بمقارنة قيمتي ثابت المرونة k نجد أنهما متساويتين في حدود أخطاء التجربة.

تصحيح التمرين الثاني: (04.00 نقاط)

I ـ 1 ـ ايجاد كل من x ، y :

لدينا:
${}^{238}_{92}\mathrm{U} \rightarrow {}^{206}_{82}\mathrm{Pb} + x\alpha + y\beta^-$

حسب قانوني الانحفاظ (العدد الكتلي والعدد الذري):

$$\left\{ \begin{array}{l} 238 = 206 + 4x \\ 92 = 82 + 2x - y \end{array} \right. \Rightarrow \left\{ \begin{array}{l} x = 8 \\ y = 6 \end{array} \right.$$

ومنه:

$${}^{238}_{92}\mathrm{U} \rightarrow {}^{206}_{82}\mathrm{Pb} + 8\alpha + 6\beta^-$$

2 ـ تبيان أن: m_Pb(t) = 0,866.m₀(U)[1 – e^-λt]

لدينا:

$$N_0(U) = N_U(t) + N_{Pb}(t)$$$$\Rightarrow N_{Pb}(t) = N_0(U) - N_U(t)$$

وطبقًا لقانون التناقص الإشعاعي:

$$N_U(t) = N_0(U) \cdot e^{-\lambda t}$$$$\Rightarrow N_{Pb}(t) = N_0(U) \cdot (1 - e^{-\lambda t})$$

نحسب الكتلة:

$$\frac{m_{Pb}(t)}{M_{Pb}} = \frac{m_0(U)}{M_U} \cdot N_0(U) \cdot (1 - e^{-\lambda t})$$$$\Rightarrow m_{Pb}(t) = \frac{M_{Pb}}{M_U} \cdot m_0(U) \cdot (1 - e^{-\lambda t})$$

حيث:

$$\frac{M_{Pb}}{M_U} = \frac{206}{238} = 0.866$$$$\Rightarrow m_{Pb}(t) = 0.866 \cdot m_0(U) \cdot (1 - e^{-\lambda t})$$

3ـ أ ـ حساب النسبة $\gamma(t)$:

$$\gamma(t) = \frac{m_{Pb}(t)}{m_U(t)}$$$$= \frac{0.866 \cdot m_0(U) \cdot (1 - e^{-\lambda t})} {m_0(U) \cdot e^{-\lambda t}}$$$$\Rightarrow \gamma(t) = 0.866 \cdot (e^{\lambda t} - 1)$$

ب- إيجاد قيمة، $t_{1/2}$ :

من العبارة السابقة نجد :

$$\gamma(t_{1/2}) = 0.866 \left(e^{\lambda t_{1/2}} - 1 \right)$$

وبما أن :

$$\lambda t_{1/2} = \ln 2 \Rightarrow \gamma(t_{1/2}) = 0.866 \left(e^{\ln 2} - 1 \right)$$

بالاعتماد على التمثيل في محور الزمن نجد :

$$t_{1/2} = 4{,}6 \times 10^9 \ \text{ans}$$$$\Rightarrow \lambda = \frac{\ln 2}{t_{1/2}} = \frac{0{,}693}{4{,}6 \times 10^9}$$$$\Rightarrow \lambda = 1{,}507 \times 10^{-10} \ \text{ans}^{-1}$$

II ـ 1ـ إيجاد $x$، $y$ وتصنيف التحول:

لدينا:

$$\frac{238}{92}U + x \ ^1_0n \longrightarrow \frac{241}{94}Pu + y \ ^0_{-1}e$$

حسب قانوني الانحفاظ لصودي:

$$\begin{cases} 238 + x = 241 \Rightarrow x = 3 \\ 92 = 94 - y \Rightarrow y = -2 \end{cases}$$

هذا التحول ليس انشطارا لأنه لم يتم فيه ظهور نوى أخف من نواة التفاعل، وليس اندماجاً لأنه لم يتم التحام نواتين خفيفتين، ولا بد أنه تفاعل نووي يحدث لأنه قد تم قذف نواة اليورانيوم بنيوترونات، وبالتالي فهو ليس ضمن أي نوع مما سبق من التفاعلات السابقة.

2 ـ معادلة التفكك المنمذج للتحول:

$$\frac{241}{94}Pu \rightarrow \frac{241}{95}Am^* + ^0_{-1}e + ^A_ZX$$

حسب قانوني الانحفاظ لصودي:

$$\begin{cases} 241 = 241 + A \Rightarrow A = 0 \\ 94 = 95 + Z \Rightarrow Z = -1 \end{cases} \Rightarrow ^A_ZX = ^0_{-1}e$$

ومنه تصبح المعادلة:

$$\frac{241}{94}Pu \rightarrow \frac{241}{95}Am^* + ^0_{-1}e$$

ثم تتخلص نواة الأمريكيوم من الاثارة بتحرير اشعاع غاما حسب المعادلة:

$$\frac{241}{95}Am^* \rightarrow \frac{241}{95}Am + 0\gamma$$

تصنيف الإشعاع:
$\beta^-$: متوسط النفاذية،
$\gamma$: عالي النفاذية.

3 ـ حساب $\lambda$، $A_0$

حسب قانون النشاط الاشعاعي لدينا:

$$\begin{cases} A_1 = A_0 e^{-\lambda t_1} \\ A_2 = A_0 e^{-\lambda t_2} \end{cases}$$

نقسم:

$$\frac{A_1}{A_2} = e^{\lambda(t_2 - t_1)} \Rightarrow \lambda = \frac{1}{t_2 - t_1} \ln\left( \frac{A_1}{A_2} \right)$$

نعوض:

$$\lambda = \frac{1}{5 - 3} \ln\left( \frac{3.4 \times 10^9}{3.08 \times 10^9} \right) = 0.0494$$

ومنه:

$$A_0 = A_1 \cdot e^{\lambda t_1}$$$$\Rightarrow A_0 = 3{,}4 \times 10^9 \cdot e^{0{,}0494 \times 3}$$$$\Rightarrow A_0 = 3{,}943 \times 10^9 \ \text{Bq}$$

نلاحظ أن قيمة النشاط الابتدائي للبلوتونيوم 241 عالية جدا (3.943 مليار تفكك في الثانية الواحدة)، وهو ما ذكره نص التمرين.

تصحيح التمرين الثالث: (06.00 نقاط)

I- دراسة عمود كهروكيميائي:

1- الرمز الاصطلاحي للعمود:

(-) Pb/Pb²⁺//Ag⁺/Ag (+)

2- الشكل ينقصه الجسر الملحي حتى يمر التيار في الناقل الأومي:

✓ إكمال العمود وتحديد جهة التيار والإلكترونات:

3- كتابة المعادلتين النصفيتين الإلكترونيتين للتفاعلات التي تحدث عند المسربين ومعادلة التفاعل: أكسدة ـ إرجاع.

• عند القطب الموجب:

  $$2\left(\text{Ag}^+_{(aq)} + e^- = \text{Ag}_{(s)}\right)$$

• عند القطب السالب:

  $$\text{Pb}_{(s)} = \text{Pb}^{2+}_{(aq)} + 2e^-$$

• معادلة التفاعل: أكسدة ـ إرجاع.

  $${\text{Pb}}_{(s)}+2{\text{Ag}}_{(aq)}^{+}={\text{Pb}}_{(aq)}^{2+}+2{\text{Ag}}_{(s)}$$

4- حساب كسر التفاعل الإبتدائي، وتعيين جهة التطور التلقائي للعمود:

$$Q_r = \frac{[\text{Pb}^{2+}]}{[\text{Ag}^+]^2} = \frac{C_1}{(C_2')^2} = \frac{0.2}{(0.1)^2} = 20$$

تحديد جهة تطور الجملة الكيميائية:
بما أن $K < Q_r$، فإن الجملة تتطور في الاتجاه المباشر.

5 ـ أ ـ حساب كمية الكهرباء:

$$Q = I \cdot \Delta t = 0{,}05 \cdot 3600 = 360 C$$

ب ـ تغير التراكيز بعد ساعتين:

لدينا:

$$x = \frac{Q}{F} = \frac{360}{96500} = 1{,}865 \cdot 10^{-2} \ \text{mol}$$

ومنه:

$$[\text{Pb}^{2+}](t) = \frac{C_1' V + x}{V}$$$$= \frac{0{,}04 + 1{,}865 \cdot 10^{-2}}{0{,}2} = 0{,}21 \ \text{mol/L}$$

ومنه:

$$[\text{Ag}^+](t) = \frac{C_2' V - 2x}{V}$$$$= \frac{0{,}02 - 3{,}73 \cdot 10^{-2}}{0{,}2} = 8{,}135 \cdot 10^{-2} \ \text{mol/L}$$

II- ثنائي القطب $RL$:

1- رسم الدارة وتوجيه التيار والتوترات.

2- إثبات المعادلة التفاضلية لـ $u_s(t)$:

لدينا:

$$u_s(t) = u_R(t) - u_b(t)$$

نشتق الطرفين:

$$\Rightarrow \frac{du_s(t)}{dt} = \frac{du_R(t)}{dt} - \frac{du_b(t)}{dt} \tag{01}$$

في البداية يجب إيجاد المعادلة التفاضلية بدلالة
$u_b(t)$ و $u_R(t)$، 

حسب قانون جمع التوترات.

$u_R + u_b = E$

$$u_R + L \frac{di}{dt} = E \quad / \frac{di}{dt} = \frac{1}{R} \frac{du_R}{dt}$$$$\Rightarrow u_R + L \frac{1}{R} \frac{du_R}{dt} = E$$$$\Rightarrow \frac{du_R}{dt} + \frac{R}{L} u_R = \frac{R}{L} E \quad \ldots (02)$$

• وبنفس الطريقة نجد:

$$u_R + u_b = E$$$$\Rightarrow R i + u_b = E$$$$\Rightarrow R \frac{di}{dt} + \frac{du_b}{dt} = 0 \quad / \frac{1}{L} \frac{du_b}{dt}$$$$\Rightarrow R \frac{1}{L} \frac{du_b}{dt} + \frac{du_b}{dt} = 0$$$$\Rightarrow \frac{du_b}{dt} \left( \frac{R}{L} + \frac{1}{L} \right) = 0 \quad \ldots (03)$$

بطرح (03) من (02) نجد:

$$\frac{du_R}{dt} + \frac{R}{L} u_R - \left( \frac{du_b}{dt} + \frac{R}{L} u_b \right) = \frac{R}{L} E$$$$\Rightarrow \left( \frac{du_R}{dt} - \frac{du_b}{dt} \right) + \frac{R}{L} \left( u_R - u_b \right) = \frac{R}{L} E$$$$\Rightarrow \frac{du_s}{dt} + \frac{R}{L} u_s = \frac{R}{L} E \quad \ldots (04)$$

3 ـ ايجاد عبارة الثوابت A ، B ، C :

$$u_s(t) = A - C e^{-\frac{t}{\tau}} \quad \ldots (05)$$$$\frac{du_s(t)}{dt} = B C e^{-\frac{t}{\tau}} \quad \ldots (06)$$

نعوض (05) و (06) في (04) فنجد:

$$B C e^{-\frac{t}{\tau}} + \frac{1}{\tau}(A - C e^{-\frac{t}{\tau}}) = \frac{E}{\tau}$$$$\Rightarrow B C e^{-\frac{t}{\tau}} + \frac{A}{\tau} - \frac{C}{\tau} e^{-\frac{t}{\tau}} = \frac{E}{\tau}$$$$\Rightarrow C e^{-\frac{t}{\tau}}(B - \frac{1}{\tau}) + \frac{A}{\tau} = \frac{E}{\tau}$$

بما أن المعادلة (05) حلا للمعادلة (04) فإن:

$$\left\{ \begin{array}{l} \frac{A}{\tau} = \frac{E}{\tau} \Rightarrow A = E \\ C (B - \frac{1}{\tau}) = 0 \Rightarrow B = \frac{1}{\tau} \end{array} \right.$$

من الشروط الابتدائية نجد:

$$t = 0 \Rightarrow u_s(0) = -E$$$$t = 0 \Rightarrow u_s(0) = A - C = -E \Rightarrow C = 2E$$

4- اثبات أن البيان $u_s(t)$ يقطع محور الأزمنة في اللحظة $t_1 = \tau \times \ln 2$ :

لدينا:

$$u_s(t) = E - 2E e^{-\frac{t}{\tau}}$$

عند تقاطع البيان مع محور الزمن نجد: $u_s = 0$

$$0 = E - 2E e^{-\frac{t_1}{\tau}} \Rightarrow \frac{1}{2} = e^{-\frac{t_1}{\tau}}$$ومنه:
$$t_1 = \tau \ln 2$$

5- ايجاد قيمة $E$:

من البيان نجد:
$E = 6V$

$$\frac{t_1}{\ln 2} = \frac{6.92\,ms}{\ln 2} = 10ms \approx 0{,}01s$$$$R = \frac{1}{\tau} = \frac{1}{0.01} = 120\,\Omega$$

6- حساب قيمة الطاقة المختزنة في الوشيعة عند اللحظة $t_1$:

لدينا:

$$E_L(t) = \frac{1}{2} L i^2(t) = \frac{1}{2} L I_0^2 \left(1 - e^{-t/\tau} \right)^2$$

ومنه:

$$E_L(t_1) = \frac{1}{2} \cdot 1{,}2 \cdot \left(\frac{6}{120}\right)^2 \cdot \left(1 - e^{-\frac{\tau \ln 2}{\tau}} \right)^2$$$$\Rightarrow E_L(t_1) = 3{,}75 \cdot 10^{-4} \ \text{J}$$

تصحيح التمرين التجريبي: (06.00 نقاط)

I- تحضير محلول كلور الهيدروجين انطلاقا من محلول تجاري:

1- حساب قيمة التركيز المولي $(c_0)$ للمحلول التجاري:

لدينا:

$$c_0 = \frac{10 \cdot d \cdot P}{M}$$$$\Rightarrow c_0 = \frac{10 \cdot 1{,}068 \cdot 10}{36{,}5} \approx 3 \ \text{mol/L}$$

2- البروتوكول التجريبي لتحضير $V = 200 \ mL$ من المحلول الممدد $(S)$:

• ذكر الحاجيات: الأدوات ، المواد الكيميائية ، أدوات الأمان.

• طريقة العمل: نأخذ بواسطة الماصة حجما $V_0$ من المحلول $S_0$ ، ونضعه في حوجلة سعة $V = 200 \ mL$ تحتوي على كمية من الماء المقطر، نكمل حجم المحلول الناتج بالماء المقطر إلى غاية العلامة المدرجة.

• مع كتابة جميع التحذيرات الخاصة بطرق التعامل مع الحمض المركز.

II- تجربة الفوج الأول: المعايرة اللونية لمحلول حمض كلور الهيدروجين المحضر.

1- رسم التركيب التجريبي للمعايرة:

2- كتابة معادلة تفاعل المعايرة:

$$H_3O^+_{(aq)} + OH^-_{(aq)} \rightarrow 2 H_2O_{(l)}$$

3- تحديد التركيز المولي للمحلول الحمضي المحضر $(c_a)$

من علاقة التكافؤ نجد:

$$c_a V_a = c_b V_{b_E}$$$$\Rightarrow c_a = \frac{c_b V_{b_E}}{V_a} = \frac{0{,}1 \cdot 3}{20}$$$$\Rightarrow c_a = 1{,}5 \cdot 10^{-2} \ \text{mol/L}$$

استنتاج التركيز المولي $c_0$ للمحلول التجاري $(S_0)$

من علاقة التمديد نجد:

$$F = \frac{c_0}{c_a}$$$$\Rightarrow c_0 = F \cdot c_a = 200 \cdot 0{,}015$$$$\Rightarrow c_0 = 3 \ \text{mol/L}$$

4- حساب النسبة المئوية الكتلية لحمض كلور الهيدروجين في المحلول التجاري (S₀):

$$P\% = \frac{c_0 \times M}{10 \times d} = \frac{3 \times 36{,}5}{10 \times 1{,}068} = \mathbf{10{,}25\%}$$

III - تجربة الفوج الثاني: متابعة زمنية لتحول كيميائي تام بين كربونات الكالسيوم الصلبة ومحلول حمض كلور الهيدروجين التجاري المعدل.

1- إكمال بيانات التركيب التجريبي:

الرقم	01	02	03	04	05	06	07
الاسم	المزيج التفاعلي	دورق زجاجي	أنبوب انطلاق	حوض مائي	الغاز المنطلق	مخبار مدرج	ماء

جدول تقدم التفاعل:

2- حساب التركيز المولي لمحلول الحمض المعدل $c_a$، ثم نستنتج التركيز المولي $c_0$ للمحلول التجاري $(S_0)$:

* في البداية يجب حساب قيمة التقدم الأعظمي فنجد:

$$X_{\text{max}} = n_f(\text{CO}_2) = \frac{V_f(\text{CO}_2)}{V_M}$$$$= \frac{10 \cdot 10^{-3}}{22{,}4} = 4{,}46 \cdot 10^{-4} \ \text{mol}$$

ولدينا:

$$n_f(\text{CaCO}_3) = \frac{m_0}{M} - X_f$$$$= \frac{1}{100} - 4{,}46 \cdot 10^{-4} = 9{,}55 \cdot 10^{-3} \ \text{mol} \ne 0$$

ومنـه نستنتج أن المتفاعل المحد هو شوارد الهيدرونيوم $H_3O^+_{(aq)}$

ومن جدول التقدم نجد:

$$n_f(H_3O^+) = 0 \Rightarrow c_a \times V - 2X_{\text{max}} = 0$$ومنه:

$c_a = \frac{2X_{\max}}{V} = \frac{2 \times 4.46 \times 10^{-4}}{0.06}$

ومنه:

$c_a \approx 1.5 \times 10^{-2} \, \text{mol/L}$

* حساب $c_0$:

من علاقة التمديد نجد:

$$F = \frac{c_0}{c_a}$$

ومنه:

$$c_0 = F \cdot c_a$$

ومنه:

$$c_0 = 200 \times 1.5 \times 10^{-2} = 3 \text{ mol/L}$$

3- حساب النسبة المئوية الكتلية لحمض كلور الهيدروجين في المحلول التجاري (S₀):

$$P\% = \frac{c_0 \times M}{10 \times d} = \frac{3 \times 36{,}5}{10 \times 1{,}068} = \mathbf{10{,}25\%}$$

IV - تجربة الفوج الثالث: المعايرة عن طريق قياس الناقلية لمحلول حمض كلور الهيدروجين المحضر.

1- كتابة معادلة التفاعل للمعايرة:

$$\text{H}_3\text{O}^+_{(aq)} + \text{OH}^-_{(aq)} \rightarrow 2 \text{H}_2\text{O}_{(l)}$$

2- تحديد قيمة حجم محلول هيدروكسيد الصوديوم اللازم للتكافؤ بيانياً:

بالإسقاط على البيان نجد:

$$V_{bE} = 15 \text{ mL}$$

3- إيجاد التركيز المولي للمحلول الحمضي المعدل $c_a$ بطريقتين:

ط1 - من علاقة التكافؤ نجد:

لدينا:
$c_a \cdot V_a = c_b \cdot V_{b_E}$

ومنه:
$c_a = \frac{c_b \cdot V_{b_E}}{V_a} = \frac{0{,}01 \times 15}{10}$

ومنه:
$c_a = 1{,}5 \times 10^{-2} \, \text{mol/L}$

ط2 - نعتمد على قيمة الناقلية النوعية الابتدائية من البيان فنجد:

$$\sigma_0 = \left[H_3O^+\right]_0 \times \lambda_{H_3O^+} + \left[Cl^-\right]_0 \times \lambda_{Cl^-}$$$$\Rightarrow \sigma_0 = c_a \times (\lambda_{H_3O^+} + \lambda_{Cl^-})$$$$\Rightarrow c_a = \frac{\sigma_0}{\lambda_{H_3O^+} + \lambda_{Cl^-}}$$ومنـه:

$c_a = \frac{0{,}64}{35 \times 10^{-3} + 7{,}6 \times 10^{-3}}$

ومنـه:
$c_a = 15 \, \text{mol/m}^3 = 1{,}5 \times 10^{-2} \, \text{mol/L}$

حساب $c_0$:

من علاقة التمديد لدينا:

$F = \frac{c_0}{c_a}$

ومنه:
$c_0 = F \cdot c_a$

ومنه:
$c_0 = 200 \times 1{,}5 \times 10^{-2} = 3 \, \text{mol/L}$

4- حساب تراكيز مختلف الأفراد الكيميائية في المزيج عند التكافؤ: 

الأفراد الكيميائية المتواجدة في المزيج النهائي عند التكافؤ هي:

$Na^+, Cl^-, H_3O^+, OH^-, H_2O$

ومنـه:

$$\begin{cases} [\text{Na}^+]_{\text{eq}} = \dfrac{0{,}01 \times 15}{25} = 6 \times 10^{-3} \, \text{mol/L} \\ [\text{Cl}^-]_{\text{eq}} = \dfrac{0{,}015 \times 10}{25} = 6 \times 10^{-3} \, \text{mol/L} \\ [\text{H}_3\text{O}^+]_{\text{eq}} = [\text{OH}^-]_{\text{eq}} = 10^{-7} \, \text{mol/L} \end{cases}$$

- استنتاج اسم الملح الناتج وكتلته:

• الملح الناتج هو كلور الصوديوم منحلا في الماء ونُتح حسب المعادلة الاجمالية التالية:

(H₃O⁺+Cℓ^-)_(aq)+(Na⁺+OH^-)_(aq)=(Na⁺+Cℓ^-)_(aq)+2H₂O_(ℓ)

نعتمد على جدول التقدم لحساب كتلة الملح الناتجة والمنحلة في الماء فنجد:

$$n_f (\text{NaCl}) = X_{\text{éq}} = c_a \cdot V_a = c_b \cdot V_{b_E}$$

ومنـه:

$$n_f (\text{NaCl}) = 1{,}5 \times 10^{-2} \times 0{,}01$$

ومنـه:

$$n_f (\text{NaCl}) = 1{,}5 \times 10^{-4} \, \text{mol}$$

ولدينا:

$$m_f (\text{NaCl}) = n_f (\text{NaCl}) \cdot M$$

ومنـه:

$$m_f (\text{NaCl}) = 1{,}5 \times 10^{-4} \times 58{,}5$$

ومنـه:

$$m_f (\text{NaCl}) = 8{,}775 \times 10^{-3} \, \text{g}$$

5- حساب النسبة المئوية الكتلية لحمض كلور الهيدروجين في المحلول التجاري $(S_0)$:

$$P\% = \frac{c_p \times M}{10 \times d} = \frac{3 \times 36{,}5}{10 \times 1{,}068} = 10{,}25\%$$

6- من التجارب الثلاثة السابقة، نستنتج أن المعلومات المكتوبة على قنينة محلول روح الملح التجاري تتوافق مع النتائج التجريبية المتحصل عليها في كل تجربة، وعليه روح الملح التجاري المدروس غير مغشوش.

الموضوع بصيغة الـ PDF

الحل بصيغة الـ PDF